Визначення 1. Піраміда називається правильною, якщо її основою є правильний багатокутник, при цьому вершина такої піраміди проектується в центр її основи.
Визначення 2. Піраміда називається правильною, якщо її основа - правильний багатокутник, а висота проходить через центр основи.
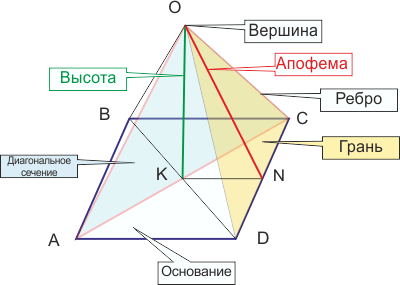
Елементи правильної піраміди
- Апофема - це висота бічної Грані, проведена з ее вершини. На малюнку позначена як відрізок ON.
- Точка, что з'єднує бічні ребра и не лежить в площіні основи, назівається вершиною піраміди (О).
- Трикутники, что ма ють спільну сторону з основою и одну з вершин, что збігається з вершиною, назіваються бічнімі гранями (AOD, DOC, COB, AOB).
- Відрізок перпендикуляра, проведеного через вершину піраміди до площини ее основи назівається висота піраміди (ОК).
- Діагональній переріз піраміди - це переріз, что проходити через вершину и діагональ основи (AOC, BOD).
- Багатокутнік, якому НЕ Належить вершина піраміди, назівається основою піраміди (ABCD).
Якщо в основі правильної піраміди лежить трикутник, чотирикутник і т.д., то вона називається правильною трикутною, чотирикутною і т.д.
Трикутна піраміда є чотирьохграннік - тетраедр..
Властивості правильної піраміди
Для вирішення завдань необхідно знати властивості окремих елементів, які в умові зазвичай опускаються, так як вважається, що учень повинен це знати спочатку.- бічні ребра рівні між собою;
- апофеми рівні;
- бічні грані рівні між собою (при цьому, відповідно, рівні їх площі, бічні сторони і основи), тобто вони є рівними трикутниками;
- всі бічні грані є рівними рівнобокими трикутниками;
- в будь-яку правильну піраміду можна як вписати, так і описати біля неї сферу.
- якщо центри вписаної і описаної сфери збігаються, то сума плоских кутів при вершині піраміди дорівнює π, а кожен з них відповідно π / n, де n - кількість сторін багатокутника основи;
- площа бічної поверхні правильної піраміди дорівнює половині твору периметра основи на апофему;
- близько основи правильної піраміди можна описати коло (див. також радіус описаного кола трикутника);
- всі бічні грані утворюють з площиною основи правильної піраміди рівні кути;
- всі висоти бічних граней рівні між собою
Вказівки до вирішення завдань. Властивості, перераховані вище, повинні допомогти в практичному вирішенні. Якщо потрібно знайти кути нахилу граней, їх поверхню і т. д., то загальна методика зводиться до розбиття всієї об'ємної фігури на окремі плоскі фігури і застосування їх властивостей для знаходження окремих елементів піраміди, оскільки багато елементів є загальними для декількох фігур.
Необхідно розбити всю об'ємну фігуру на окремі елементи - трикутники, квадрати, відрізки. Далі, до окремих елементів застосувати знання з курсу планіметрії, що істотно спрощує знаходження відповіді.
Формули для правильної піраміди
Формули для знаходження об'єму і площі бічної поверхні:
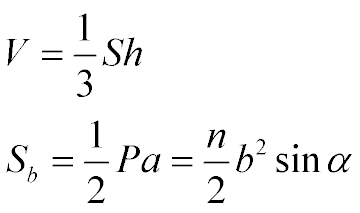
Позначення:
V - об'єм піраміди
S - площа основи
h - висота піраміди
Sb - площа бічної поверхні
a - апофема (не плутати з α)
P - периметр основи
n - число сторін основи
b - довжина бічного ребра
α - (альфа) плоский кут при вершині піраміди
S - площа основи
h - висота піраміди
Sb - площа бічної поверхні
a - апофема (не плутати з α)
P - периметр основи
n - число сторін основи
b - довжина бічного ребра
α - (альфа) плоский кут при вершині піраміди
Дана формула знаходження об'єму може застосовуватися тільки для правильної піраміди:
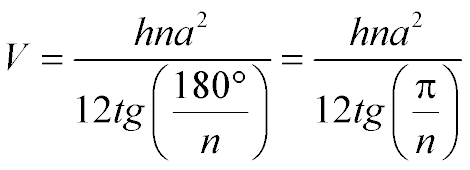 ,
,
де
V - об'єм правильної піраміди
h - висота правильної піраміди
n - число сторін правильного багатокутника, який є основою для правильної піраміди
a - довжина сторони правильного багатокутника
h - висота правильної піраміди
n - число сторін правильного багатокутника, який є основою для правильної піраміди
a - довжина сторони правильного багатокутника
Правильна усічена (зрізана) піраміда
Якщо провести розріз, паралельний основі піраміди, то тіло, укладене між цими площинами і бічною поверхнею, називається усіченою пірамідою. Це перетин для усіченої піраміди є однією з її основ.
Висота бічної грані (яка є рівнобокою трапецією), називається - апофема правильної усіченої (зрізаної) піраміди.
Зрізана піраміда називається правильною, якщо піраміда, з якої вона була отримана - правильна.
- Відстань між основами усіченої піраміди називається висотою усіченої піраміди.
- Всі грані правильної усіченої (зрізаної) піраміди є рівнобокими трапеціями
«Бенджамин Бриэль Ли всегда был очень профессионален, держал меня в курсе всего, что происходило. Если у меня были какие-либо вопросы, он всегда был готов ответить. Это была моя первая покупка дома, я мало что знал о процессе кредитования, он помог мне понять, о чем у меня возникли вопросы. Мне очень понравилось с ним работать.
ОтветитьУдалитьОн - специалист по кредитам, работающий с группой инвесторов, которые готовы профинансировать любой проект или одолжить вам любую сумму под очень низкий процент.
Свяжитесь с Бенджамином Бриэлем Ли. Электронная почта: lfdsloans@outlook.comWhats-App Number: + 1-989-394-3740.